The Effect of Interactions on a Topological Insulator
In this problem we will explore a concept in condensed matter physics known as topological insulators. The best way to get a sense of what they are is through the use of band theory.
We are going to use the fact that we can organize the energy eigenstates of an electron in a periodic potential according to its quasi-momentum--or wave vector--which we denote by $\mathbf{k} = (k_1, \ldots, k_d)$, and that the energy eigenvectors--or Bloch wave functions--which we denote by $u_\mu(\mathbf{k})$, depend continuously on $\mathbf{k}$. Here $\mu$ is the band index, but let us focus on one band for the moment. Crucially, each $k_i$ is defined "periodically", meaning $k_i = - \pi$ and $k_i = \pi$ should be identified, so that it really forms a circle rather than a line. The catch for topological insulators is that $u_\mu(\mathbf{k})$ can develop some "twist" as one dials $k_i$ around the circle, much like how the Möbius strip develops a twist as one goes around its waist.

As a result of these "twists", even if we completely fill a number of bands to form an insulator, some peculiar features remain. For one, we can get non-dissipative currents of some sort on the edge of the system. This is striking because it runs counter to the insulating behavior predicted by band theory, but reconcilable because the latter only implies an insulating behavior in the bulk and the current here is on the edge. One example relevant to us is given by 2-dimensional quantum spin Hall (QSH) systems, whose edge carries counter-propagating currents of opposite spins. You can read more about QSH systems here, but we will not need the details in what follows.
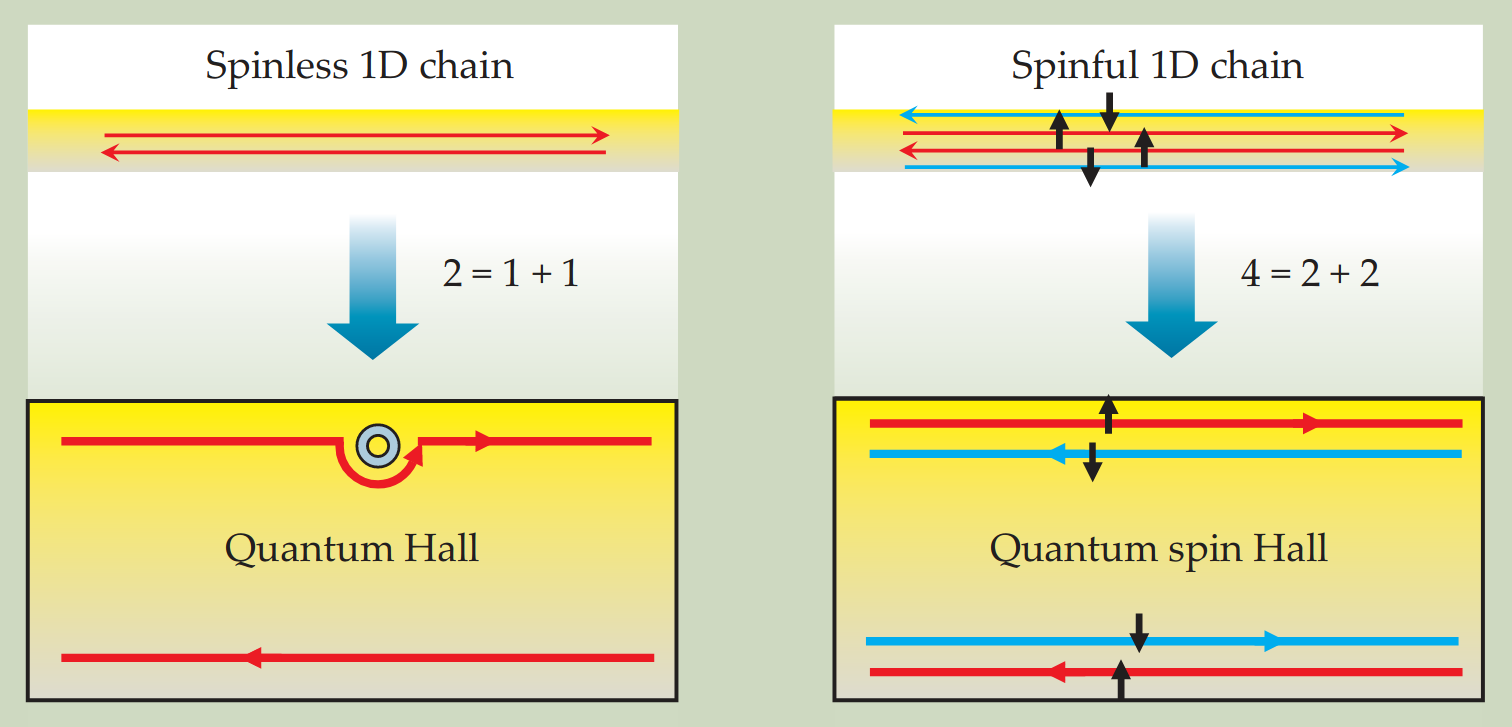
(a) A spinless one-dimensional system has both a forward and a backward mover. Those two basic degrees of freedom are spatially separated in a QH bar, as illustrated by the symbolic equation "2 = 1 + 1." The upper edge contains only a forward mover and the lower edge has only a backward mover. The states are robust: They will go around an impurity without scattering.
(b) A spinful 1D system has four basic channels, which are spatially separated in a QSH bar: The upper edge contains a forward mover with up spin and a backward mover with down spin, and conversely for the lower edge. That separation is illustrated by the symbolic equation "4 = 2 + 2."
Source: Qi, Zhang. The quantum spin Hall effect and topological insulators. [arXiv:1001.1602].
A more systematic approach to topological insulators would take symmetry into consideration. There are 10 symmetry classes (more precisely, 2 for topological insulators and 8 for topological superconductors), depending on the existence or not of time-reversal and charge conservation symmetries and exactly how they act on physical states. We will focus the Altland-Zirnbauer class AII, which has a charge conservation symmetry $U(1)$ and a time-reversal symmetry $\mathcal{T}$ squaring to $-1$.
Take a look at Table I in Schnyder et al., PRB 78, 195125 (2008) and answer the following question:
- What is the classification of 2-dimensional topological insulators in class AII? (Answer in either of the following forms: $Z$, or $Z_n$ where $n$ is an integer.)
- What is the classification of 3-dimensional topological insulators in class AII? (Answer in either of the following forms: $Z$, or $Z_n$ where $n$ is an integer.)
These classifications count how many qualitatively distinct (e.g. the presence or absence of edge modes, or exactly what kind of edge modes) types of topological insulators there are that respect a given symmetry. For instance, a $\mathbb{Z}_2$ classification would mean there are two types: a trivial type represented by $0\in \mathbb{Z}_2$ and a nontrivial type represented by $1\in \mathbb{Z}_2$.
Symmetries like charge conservation and time-reversal are internal symmetries, in that they do not involve any spatial transformations like rotations or reflections. Recently, people have been trying to expand the list of symmetry classes by incorporating spatial symmetries. Here we will discuss one such example: glide reflection, which by definition is a translation followed by a reflection. In Cartesian coordinates, we can write it as $$ (x,y,z) \rightarrow (x+1/2, -y, z) $$ We can then ask how many qualitatively distinct types of topological insulators there are that respect the glide symmetry in addition to the usual symmetries $U(1)$ and $\mathcal{T}$ of class $\mathcal{AII}$. This question has been answered by Shiozaki et al.. Take a look at that paper and answer the following question:
- What is the classification of 3-dimensional topological insulators in class $\mathcal{AII}$ that respect an additional glide symmetry? (Answer in either of the following forms: $Z$, or $Z_n$ where $n$ is an integer.)
- $\alpha$ is injective;
- $\beta$ is surjective;
- the image of $\alpha$ equals the kernel of $\beta$.
These conditions, together with the known $A$, $B$, and $C$, fix the homomorphisms $\alpha$ and $\beta$ completely. You may need a little time to get used to the workings of abelian groups, homomorphisms, short exact sequences, etc. When you think you have grasped the concepts, try answering the following questions.
- If we write the elements of $\mathbb{Z}_n$ as $0,1, ..., n-1$ and the elements of $\mathbb{Z}$ as $0, \pm 1, \pm 2, ...$, then what is $\alpha(1)$?
- In the same notation, what is $\beta(1)$?
Physically, the homomorphism $\alpha$ corresponds to an "alternating-layer construction." It takes a 2-dimensional topological insulator that respects $U(1)$ and $\mathcal{T}$ as input, and returns a 3-dimensional topological insulator that respects glide as well as $U(1)$ and $\mathcal{T}$ as output, by layering the 2-dimensional system in an alternating fashion as illustrated here:
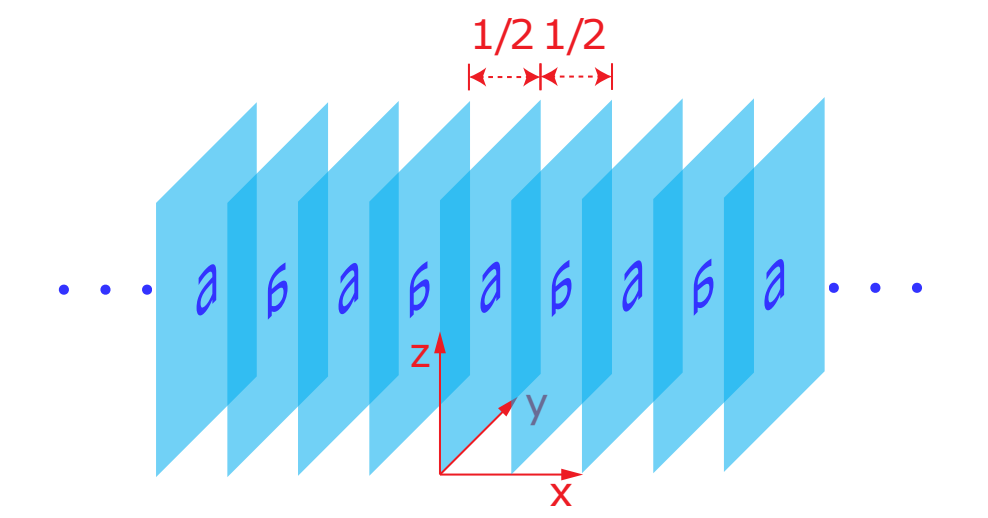
In particular, it maps the element $1$ of $A$, which corresponds to quantum spin Hall systems, to the so-called "hourglass-fermion" phase. The latter has surface modes (the one higher-dimensional analog of edge modes) that look literally like an hourglass, as can be seen here. The homomorphism $\beta$, on the other hand, is given by relaxing the glide symmetry constraint.
Band theory unfortunately applies only to non-interacting electrons, yet we know that electrons interact via the Coulomb potential. In many cases, results from band theory approximate the physics quite well, but it would be reassuring to prove this explicitly. In particular, we would like to know if the nontrivial elements of $B$ are robust to interactions, in the sense that their peculiar surface modes cannot be destroyed by interactions. Now, a result of arXiv:1709.06998 [cond-mat.str-el] is that if an element $a\in A$ is robust to interactions, then so is the element $\alpha(a) \in B$. Another result of the same work is that if for a given element $b\in B$, $\beta(b)$ is robust to interactions, then so is $b$ itself. Using these results, convince yourself that all nontrivial elements of $B$ are robust to interactions.